Derivatives of Inverse Trigonometric Functions

What you will learn:

In this lesson we will look at inverse trigonometric functions and their derivatives.

You will find it useful to work through the examples using pencil and paper; and then to try to recreate them yourself.

This is a necessarily a long lesson, as we try to give a full explanation of how the graphs of inverse functions arise and how we find the derivatives of the inverse functions.

Inverse Trigonometric Functions

We have come across the inverse sine, cosine and tangent from as far back as National 4 and National 5 when we were finding angles in triangles. In Higher, we moved onto solving various Trigonometric equations with multiple solutions again using the inverse trigonometric ratios.

If we found that, for example, $$\text{sin } x = 0.5$$ Then to find $x$, we used the inverse sine function:$$ x = \text{sin}^{-1} \ 30^{\circ} $$and we accessed this using the SHIFT or 2nd FUNCTION key on the calculator.

We also had to determine which quadrant the angle $x$ was in. We used ASTC and since, in the above case, $\text{sin }x$ is positive, then $x$ has to be in either the first or second quadrant. We determined which one of these from further information included in the question.

---

Notation for Inverse Trigonometric Functions

The notation for inverse trigonometric functions can vary.

In mathematics when we are writing down our working we refer to the inverse functions as: $$ f(x) = \text{sin}^{-1}\ x \quad \quad f(x) = \text{cos}^{-1}\ x \quad \quad f(x) = \text{tan}^{-1} \ x\\[12pt] f(x) = \text{cosec}^{-1}\ x \quad \quad f(x) = \text{sec}^{-1}\ x \quad \quad f(x) = \text{cot}^{-1} \ x $$However on some calculators, spreadsheets and mathematical programs we would refer to the functions using the notation: $$ \text{ASIN}() \quad \quad \text{ACOS}() \quad \quad \text{ATAN}() $$also in spreadsheets such as Excel, to find $\text{sec}^{-1}\ x$ one would use the reciprocal ~ $\large \frac{1}{ACOS()}$ and so on.

Other notations use: $$ \text{arcsin }x \quad \quad \text{arccos }x \quad \quad \text{arctan }x \\[12pt] \text{arccosec }x \quad \quad \text{arcsec }x \quad \quad \text{arccot }x $$In this course we shall use the notation: $$ f(x) = \text{sin}^{-1}\ x \quad \quad f(x) = \text{cos}^{-1}\ x \quad \quad f(x) = \text{tan}^{-1} \ x \quad etc. $$It is important to note that $\text{sin}^{-1} x$ means the inverse of $\text{sin }x\ $ and NOT the reciprocal which would be written as $(\text{sin }x)^{-1}$. Some background information on the naming convention and other facts about the inverse trigonometric function can be found: here at Wikipedia.

There is much debate as to whether the form $y = \text{sin}^{-1} \ x$ is an acceptable notation because it may be confused with the reciprocal, and those of this opinion suggest that $y=\text{arcsin } x$, etc. should be used.

---

Graphs of Inverse Trigonometric Functions

We are familiar with the graphs of the standard trigonometric functions: sine, cosine, tangent, cosecant, secant and cotangent. So what do the graphs of the inverse functions look like.

For an inverse function to exist, there must be a one-to-one correspondence between the graph of the inverse function and the original function. For this to work, we must restrict the domain of the original function, which results in an appropriate restriction of the range of the inverse function

There are many ways to restrict the domain of functions to create this one-to-one correspondence so that the inverse will exist. However, there is a generally agreed upon interval which is: $$ \left[ -\frac{\pi}{2}, \ \pi \right] $$Although this covers three quadrants, we can only choose two of these to form our restriction.

The above interval is split so that the domain of the original function (the range of the inverse function) starts at either: $\large -\frac{\pi}{2}$ or $0$ (but not both).

If it starts at $-\Large \frac{\pi}{2}$ it ends at $\Large\frac{\pi}{2}$, so the interval is: $\left( -\Large\frac{\pi}{2}\normalsize, \ \Large \frac{\pi}{2} \right)$.

If it starts at $0$ then it ends at $\pi$ so the interval is: $\left( 0, \ \pi \right)$.

Within this interval there may be discontinuities or certain values that have to be excluded - for example where there is a division by $0$. In some cases the end-points are excluded.

We will study the graphs of these functions and see how the inverse functions are constructed. If you want to know more about how the decision regarding the domain is reached click on the following link:   Onlinemath4all.com

---

Graph of the Inverse Sine Function

First we will look at the graph of $y = \text{sin }x$.

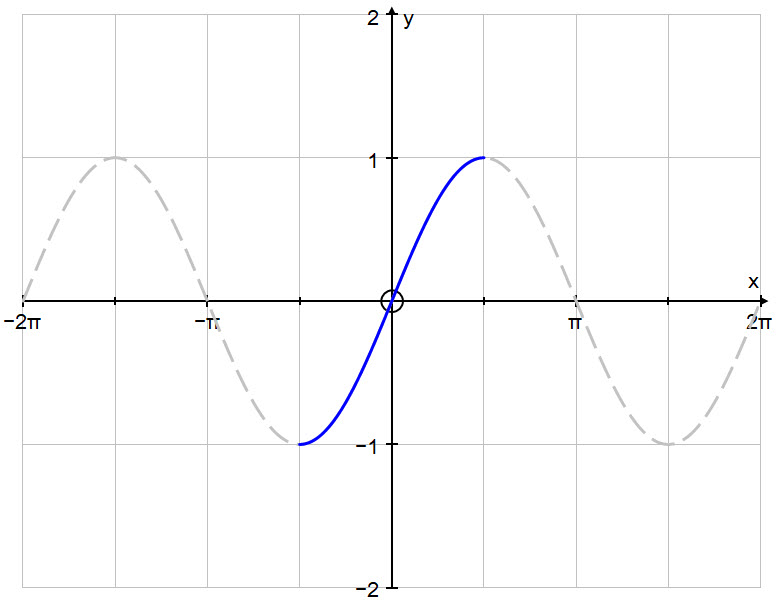
By restricting the domain of the function $y = \text{sin }x$ to $- \large \frac{\pi}{2} \normalsize \ \le \ x \ \le \large \frac{\pi}{2}\ $ we can create a one-to-one correspondence over the whole of the codomain (range) of the function such that $-1 \ \le \ y \ \le \ 1$.

In this way, by extension, we also restrict the domain of the inverse function $y = \text{sin}^{-1}\ x$ so that it will only evaluate to a single value, called its principal value.

Recall that the graph of the inverse function is a reflection of the graph of the original function in the line $y = x$.

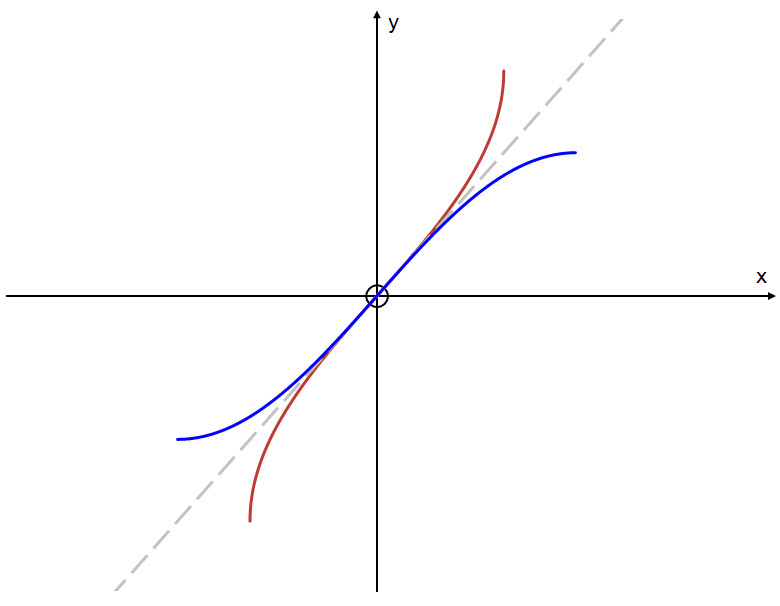
Below is the graph of the inverse function: $y = \text{sin}^{-1} \ x$.

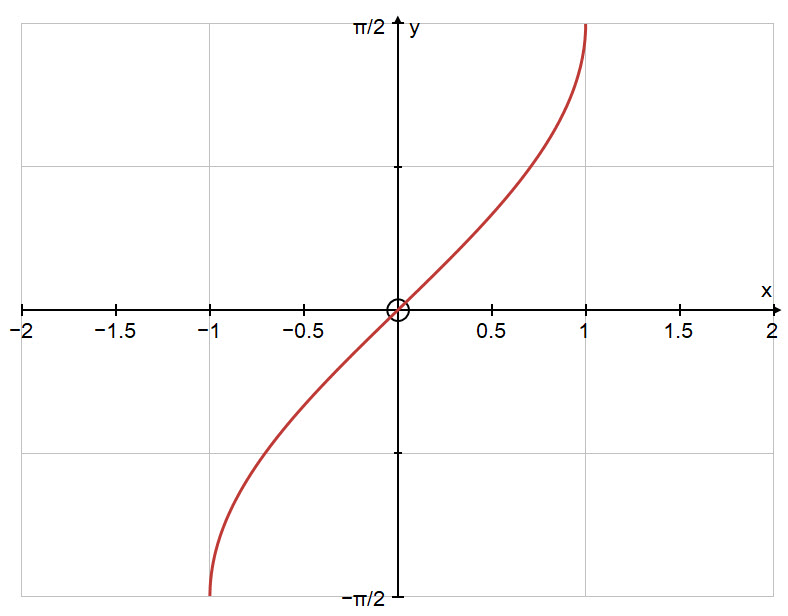
The domain of the inverse function is: $-1 \ \le \ x \ \le \ 1$.

The codomain or range of the inverse function is: $-\large \frac{\pi}{2} \normalsize \ \le \ y \ \le \ \large \frac{\pi}{2}$.

---

Graph of the Inverse Cosine Function

First we will look at the graph of $y = \text{cos }x$.

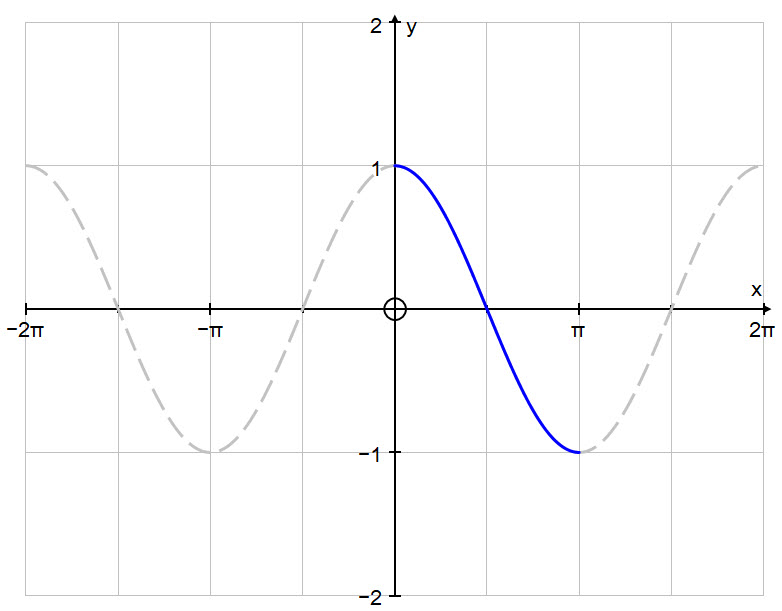
By restricting the domain of the function $y = \text{cos }x$ to $0 \ \le \ x \ \le \pi$ we can create a one-to-one correspondence over the whole of the codomain (range) of the function such that $-1 \ \le \ y \ \le \ 1$.

In this way, by extension, we also restrict the domain of the inverse function $y = \text{cos}^{-1}\ x$ so that it will only evaluate to a single value, called its principal value.

Recall that the graph of the inverse function is a reflection of the graph of the original function in the line $y = x$.

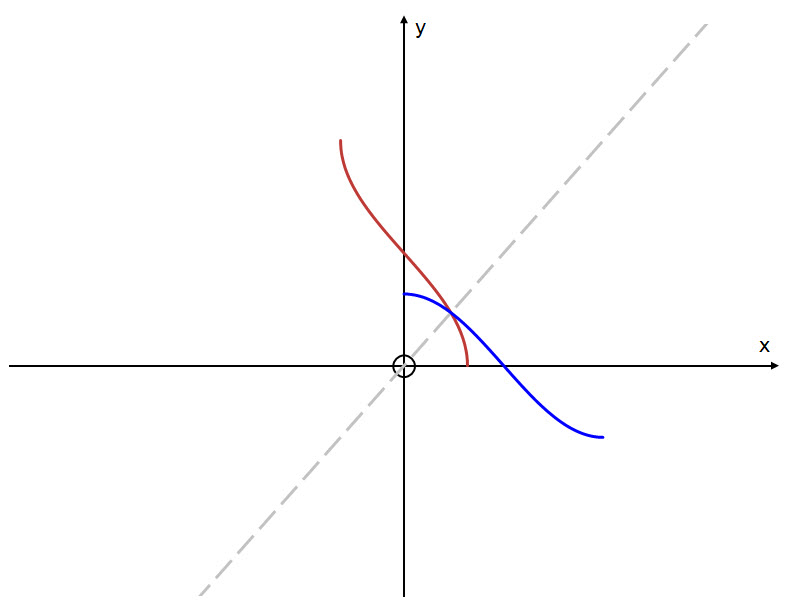
Below is the graph of the inverse function: $y = \text{cos}^{-1} \ x$.

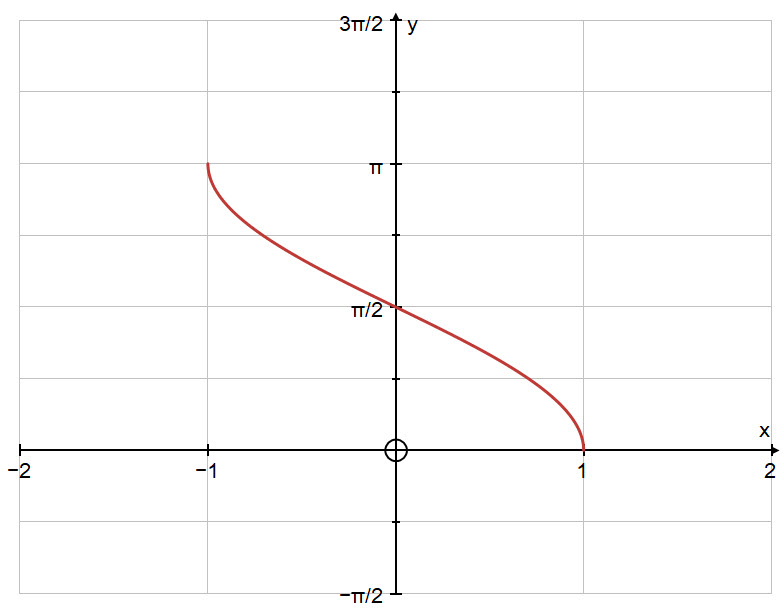
The domain of the inverse function is: $-1 \ \le \ x \ \le \ 1$.

The codomain or range of the inverse function is: $0 \ \le \ y \ \le \ \pi$.

---

Graph of the Inverse Tangent Function

First we will look at the graph of $y = \text{tan }x\ $.

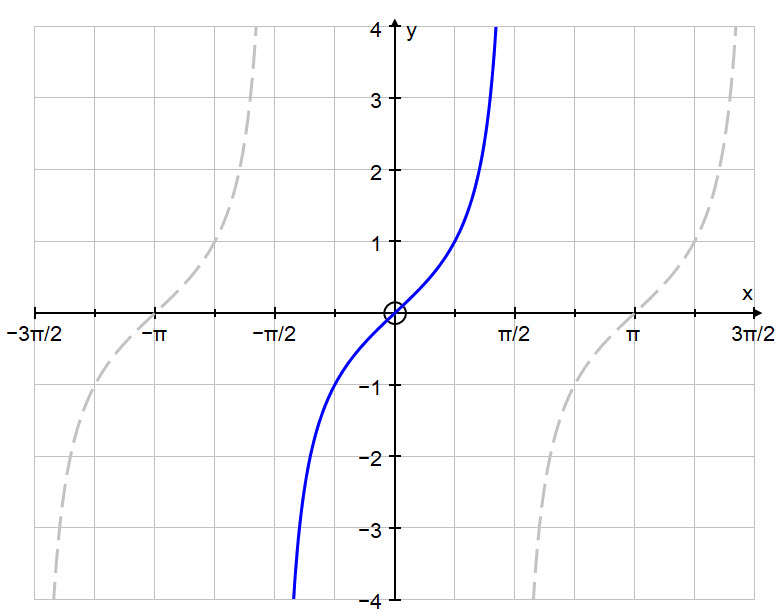
By restricting the domain of the function $y = \text{tan }x$ to $\ \large -\frac{\pi}{2} \normalsize \ \lt \ x \ \lt \large \frac{\pi}{2}\ $ we can create a one-to-one correspondence over the whole of the codomain (range) of the function such that $-\infty \ \lt \ y \ \lt \ \infty$.

In this way, by extension, we also restrict the domain of the inverse function $y = \text{tan}^{-1}\ x$ so that it will only evaluate to a single value, called its principal value.

Recall that the graph of the inverse function is a reflection of the graph of the original function in the line $y = x$.

Below is the graph of the inverse function: $y = \text{tan}^{-1} \ x$.

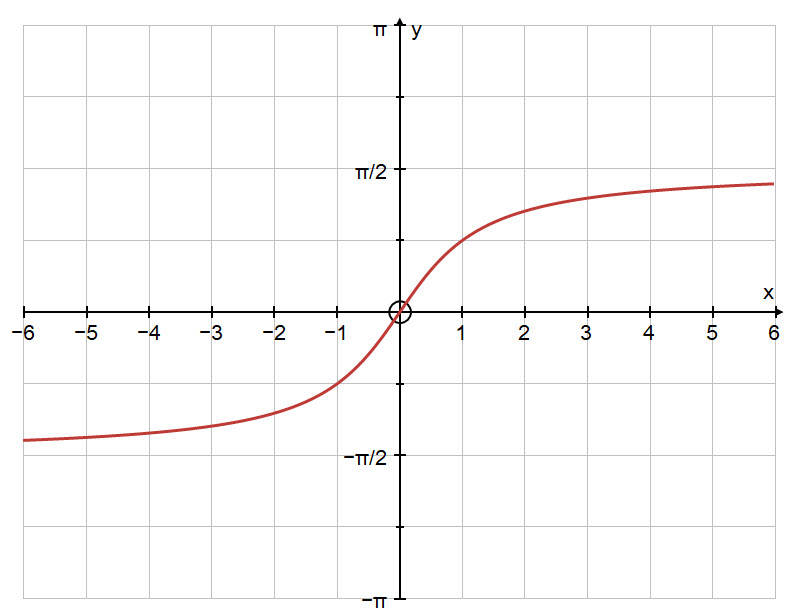
The domain of the inverse function is: $-\infty \ \lt \ x \ \lt \ \infty$.

The codomain or range of the inverse function is: $- \large \frac{\pi}{2} \normalsize \ \lt \ y \ \lt \ \large \frac{\pi}{2} $.

---

Derivatives of the Inverse Functions

Recall our formula for the Reciprocal Derivative: $$ \frac{dy}{dx} \ = \ \frac{1}{\Large\frac{dx}{dy}} \quad ... \quad (1) $$

Derivative of sin^-1 x

$$ \text{Let } \ \ y = \text{sin}^{-1}\ x \\[12pt] \implies \quad x = \text{sin }y \quad ... \quad (2)\\[12pt] $$Differentiate with respect to $y$: $$ \implies \quad \frac{dx}{dy} \ = \ \text{cos }y $$Using the formula (1) above: $$ \implies \quad \frac{dy}{dx} \ = \ \frac{1}{\text{cos }y}\quad ... \quad (3)\\[12pt] $$Using the Pythagorean Identity $\ \text{sin}^2\ y + \text{cos}^2\ y = 1$: $$ \implies \ \text{cos }y = \sqrt{\mathstrut{1-\text{sin}^2\ y}} $$Substituting for $\text{cos }y$ in equation (3): $$ \implies \quad \frac{dy}{dx} \ = \ \frac{1}{\sqrt{\mathstrut{1-\text{sin}^2\ y}}} $$But we know from (2) that $\ x = \text{sin }y$, so: $$ \implies \quad \frac{dy}{dx} \ = \ \frac{1}{\sqrt{\mathstrut{1-x^2}}}\\[24pt] \color{red}{\text{Hence if: }\quad y = \text{sin}^{-1}\ x \quad \text{then} \quad \frac{dy}{dx} \ = \ \frac{1}{\sqrt{\mathstrut{1-x^2}}}} $$

---

Proceeding in a similar way, we shall condense the working and find the derivatives of the inverse cosine and inverse tangent functions:

Derivative of cos^-1 x

$$ \text{Let } \ \ y = \text{cos}^{-1}\ x \\[12pt] \implies \quad x = \text{cos }y \\[12pt] \implies \quad \frac{dx}{dy} \ = \ -\text{sin }y \\[12pt] \implies \quad \frac{dy}{dx} \ = \ -\frac{1}{\text{sin }y}\\[12pt] $$Using the Pythagorean Identity $\ \text{sin}^2\ y + \text{cos}^2\ y = 1$: $$ \implies \ \text{sin }y = \sqrt{\mathstrut{1-\text{cos}^2\ y}} \implies \quad \frac{dy}{dx} \ = \ \frac{1}{\sqrt{\mathstrut{1-\text{cos}^2\ y}}} $$But we know that $\ x = \text{cos }y$, so: $$ \implies \quad \frac{dy}{dx} \ = \ -\frac{1}{\sqrt{\mathstrut{1-x^2}}}\\[24pt] \color{red}{\text{Hence if: }\quad y = \text{cos}^{-1}\ x \quad \text{then} \quad \frac{dy}{dx} \ = \ -\frac{1}{\sqrt{\mathstrut{1-x^2}}}} $$

---

Derivative of tan^-1 x

$$ \text{Let } \ \ y = \text{tan}^{-1}\ x \\[12pt] \implies \quad x = \text{tan }y \\[12pt] \implies \quad \frac{dx}{dy} \ = \ \text{sec}^2\ y \\[12pt] \implies \quad \frac{dy}{dx} \ = \ \frac{1}{\text{sec}^2\ y}\\[12pt] \implies \quad \frac{dy}{dx} \ = \ \text{cos}^2\ y \\[12pt] $$Now we know that for $0\ \le \ y \ \lt \large \frac{\pi}{2}$ there exists a triangle as shown below with sides such that $\text{tan }y = x$:

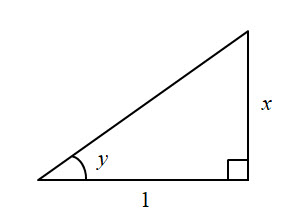
Using Pythagoras' Theorem the hypotenuse is $\sqrt{\mathstrut{1 + x^2}}$.

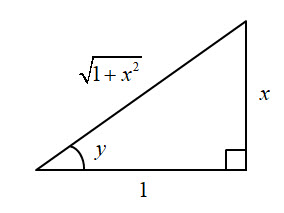
$$ \implies \text{cos }y \ = \ \frac{1}{\sqrt{\mathstrut{1 + x^2}}}\\[18pt] \implies \text{cos}^2 \ y \ =\ \frac{1}{1 + x^2}\\[24pt] \color{red}{\text{Hence if: }\quad y = \text{tan}^{-1}\ x \quad \text{then} \quad \frac{dy}{dx} \ = \ \frac{1}{1+x^2}} $$

IMPORTANT

We still need to consider the case where $-\large \frac{\pi}{2}\normalsize \ \lt \ y \ \le \ 0$ there exists a triangle as shown below with sides such that $\text{tan }y = -x$. This time the angle is in the 4th quadrant and the triangle can be drawn as:

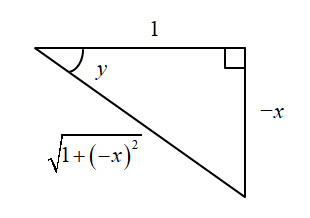
The hypotenuse this time is: $$ \sqrt{\mathstrut{1+(-x)^2}}$$ Which simplifies to: $$\sqrt{\mathstrut{1+x^2}} $$and so: $$ \implies \text{cos }y \ = \ \frac{1}{\sqrt{\mathstrut{1 + x^2}}} $$exactly the same as before.

$$ \color{red}{\text{Hence if: }\quad y = \text{tan}^{-1}\ x \quad \text{then} \quad \frac{dy}{dx} \ = \ \frac{1}{1+x^2}} $$

Remember the method for this result. We are finding lengths using Pythagoras which involves squaring, so the $(-x)^2$ will always end up positive.

---

Now we will look at the remaining three inverse trigonometric functions - the inverse cosecant, the inverse secant and the inverse cotangent.

Again we will study the graphs of these functions and see how the inverse functions are constructed. If you want to know more about how the decision regarding the domain is reached click on the following link:   Onlinemath4all.com

IMPORTANT NOTE
You are unlikely to be asked questions in the examination involving the inverse cosecant, inverse secant and inverse cotangent derivatives, but these are included for information and interest as you will likely come across these if you pursue mathematics at a higher level.

---

Graph of the Inverse Cosecant function

First we will look at the graph of $y = \text{cosec }x$.

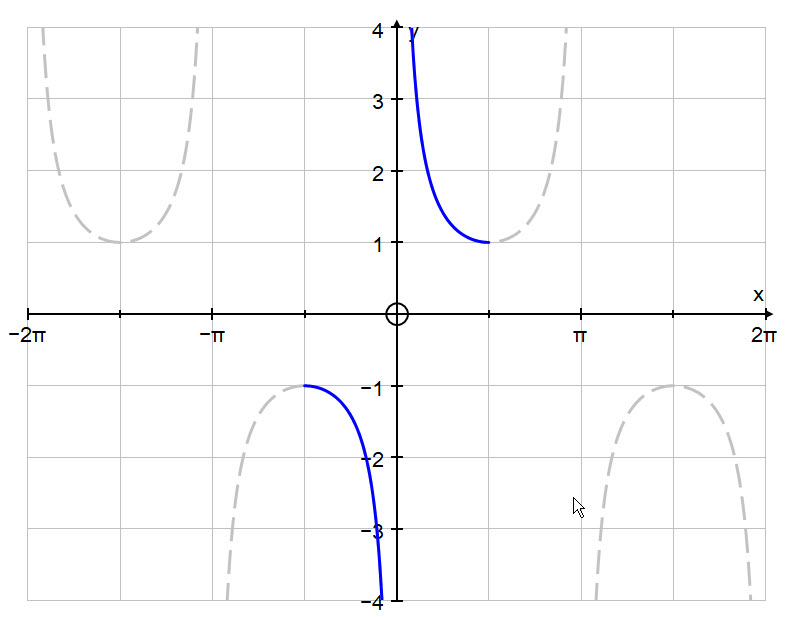
In order to make this function invertible, i.e. creating a one-to-one correspondence for an inverse function to exist, we have to restrict the domain to: $$-\frac{\pi}{2} \ \le \ x \ \lt \ 0\ \text{ AND } \ 0 \ \lt \ x \ \le \frac{\pi}{2} $$ Which we can write in set notation as: $$ x \in \left( -\frac{\pi}{2}, \ 0 \right)\ \bigcup \ \left(0, \ \frac{\pi}{2} \right) $$

Reflect $y = \text{cosec }x$ (in blue), in the line $y=x$ to obtain the graph of the inverse function $y\ = \text{cosec}^{-1}\ x$ (in red):

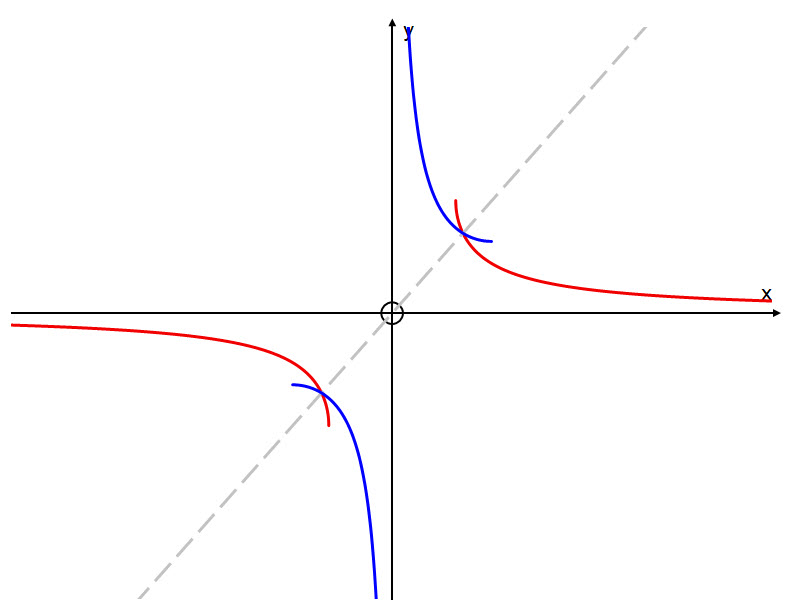
The domain of the inverse function is: $ x \in (-\infty,\ -1)\ \bigcup \ (1, \ \infty) $

The range of the inverse function is: $ y \in \left( -\frac{\pi}{2}, \ 0 \right)\ \bigcup \ \left(0, \ \frac{\pi}{2} \right) $

Note the discontinuity in both the function and its inverse.

Below is the graph of the inverse function: $\ y=\text{cosec}^{-1}\ x $.

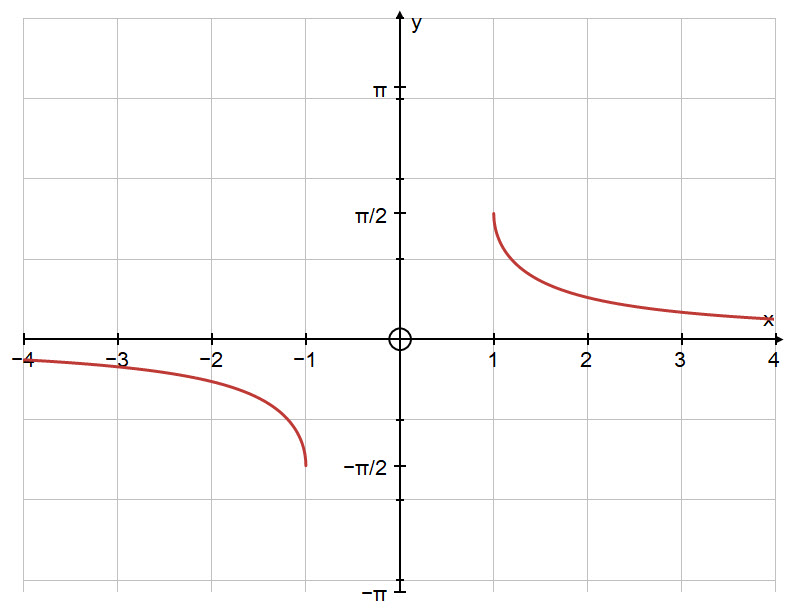
The domain of the inverse has a discontinuity from $-1$ to $1$ and its range excludes the value $0$.

The Derivative of cosec⁻¹ x

$$ \text{Let } \ \ y = \text{cosec}^{-1}\ x \\[12pt] \implies \quad x = \text{cosec }y \\[12pt] \implies \quad \frac{dx}{dy} \ = \ -\text{cosec }y\ \text{cot }y \\[12pt] \implies \quad \frac{dy}{dx} \ = \ -\frac{1}{\text{cosec }y\ \text{cot }y}\\[12pt] $$Now we know that for $0\ \le \ y \ \lt \large \frac{\pi}{2}$ there exists a triangle as shown below with sides such that $\text{cosec }y = x$:

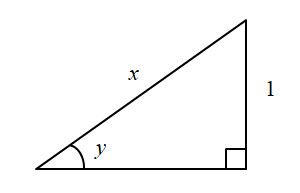
Using Pythagoras' Theorem the adjacent side is $\sqrt{\mathstrut{x^2 - 1}}$.

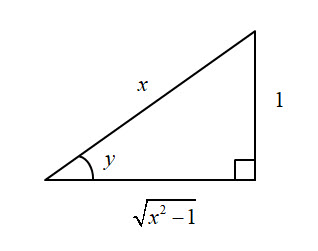
$$ \implies \text{cosec }y \ = \ x \\[18pt] \implies \text{cot } \ y \ =\ \frac{\sqrt{\mathstrut{x^2 - 1}}}{1} \ \ = \ \ \sqrt{\mathstrut{x^2 - 1}}\\[18pt] \implies \frac{dy}{dx} = - \frac{1}{x\ \sqrt{\mathstrut{x^2 - 1}} } \\[24pt] $$ Looking at the graph of the inverse function, we can see that the gradient is negative over the whole of the domain. So we have to modify our result by changing the $x$ to $|x|$ to ensure that it remains so. $$ \color{red}{\text{Hence if: }\quad y = \text{cosec}^{-1}\ x \quad \text{then} \quad \frac{dy}{dx} \ = \ -\frac{1}{|x| \ \sqrt{\mathstrut{x^2 - 1}}}} $$

IMPORTANT

As in the inverse tangent derivation, we still need to consider where $-\large \frac{\pi}{2}\normalsize \ \lt \ y \ \lt \ 0$. There exists a triangle as shown below with sides such that $\text{cosec }y = -x$. This time the angle is in the 4th quadrant and the triangle can be drawn as:

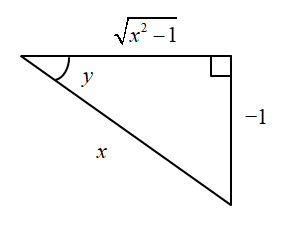
The adjacent side this time is: $$ \sqrt{\mathstrut{x^2-1}}$$ and so: $$ \implies \frac{dy}{dx} = - \frac{1}{x\ \sqrt{\mathstrut{x^2 - 1}} } \\[24pt] $$exactly the same as before. However, as $x$ is negative then this would change the sign of the derivative to a positive value.

So this is why we need to write $|x|$ in the formula to ensure that the derivative is always negative, irrespective of the sign of $x$.

$$ \color{red}{\text{Hence if: }\quad y = \text{cosec}^{-1}\ x \quad \text{then} \quad \frac{dy}{dx} \ = \ -\frac{1}{|x| \ \sqrt{\mathstrut{x^2 - 1}}}} $$

---

Graph of the Inverse Secant function

First we will look at the graph of $y = \text{sec }x$.

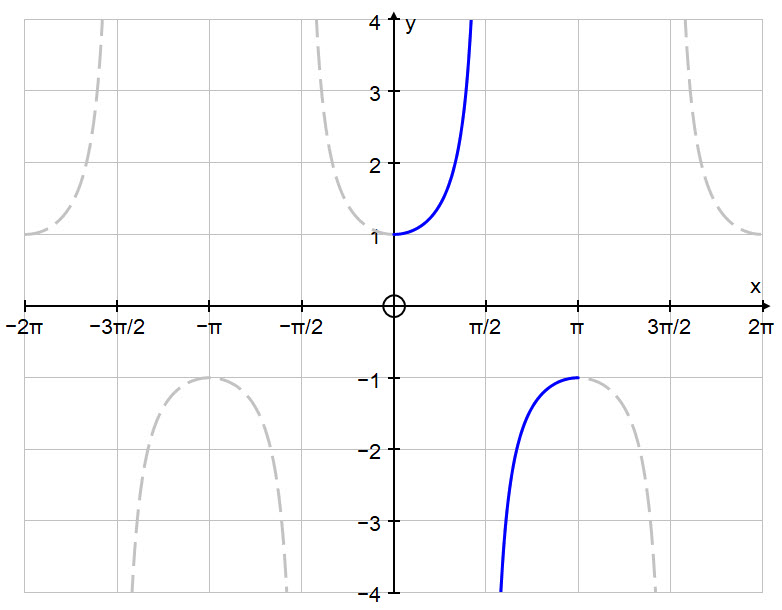
In order to make this function invertible, i.e. creating a one-to-one correspondence for an inverse function to exist, we have to restrict the domain to: $$0 \ \le \ x \ \lt \ \frac{\pi}{2}\ \text{ AND } \ \frac{\pi}{2} \ \lt \ x \ \le \pi $$ Which we can write in set notation as: $$ x \in \left( 0,\ \frac{\pi}{2} \right)\ \bigcup \ \left(\frac{\pi}{2}, \ \pi \right) $$

Reflect $y = \text{sec }x$ (in blue), in the line $y=x$ to obtain the graph of the inverse function $y\ = \text{sec}^{-1}\ x$ (in red):

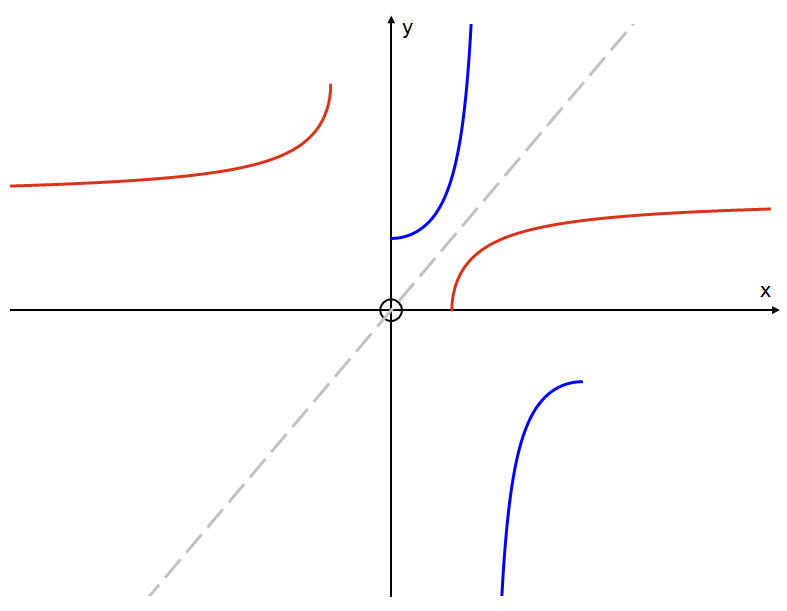
The domain of the inverse function is: $ x \in (-\infty,\ -1)\ \bigcup \ (1, \ \infty) $

The range of the inverse function is: $ y \in \left( 0, \ \frac{\pi}{2} \right)\ \bigcup \ \left( \frac{\pi}{2}, \ \pi \right) $

Note the discontinuity in both the function and its inverse.

Below is the graph of the inverse function: $\ y=\text{sec}^{-1}\ x $.

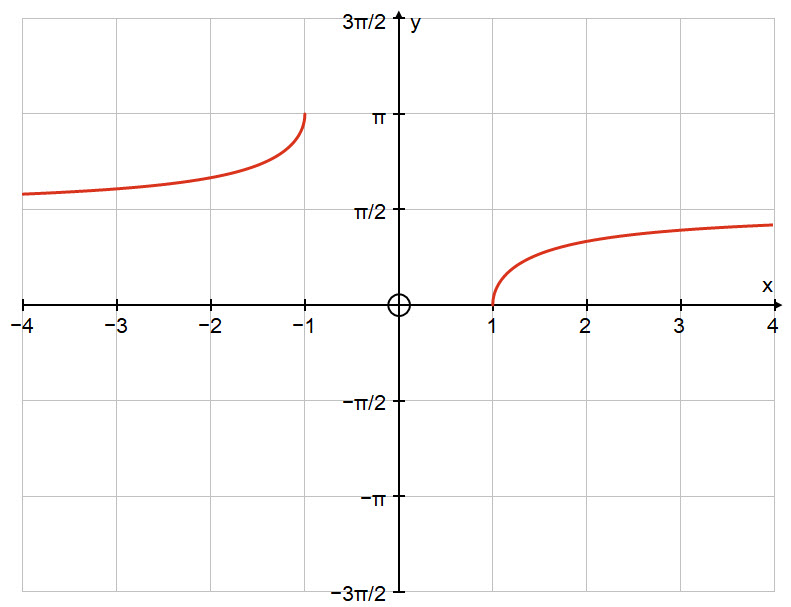
The domain of the inverse has a discontinuity from $-1$ to $1$ and its range excludes the value $\large \frac{\pi}{2}$.

The Derivative of sec⁻¹ x

$$ \text{Let } \ \ y = \text{sec}^{-1}\ x \\[12pt] \implies \quad x = \text{sec }y \\[12pt] \implies \quad \frac{dx}{dy} \ = \ \text{sec }y\ \text{tan }y \\[12pt] \implies \quad \frac{dy}{dx} \ = \ \frac{1}{\text{sec }y\ \text{tan }y}\\[12pt] $$Now we know that for $0\ \le \ y \ \lt \large \frac{\pi}{2}$ there exists a triangle as shown below with sides such that $\text{sec }y = x$:

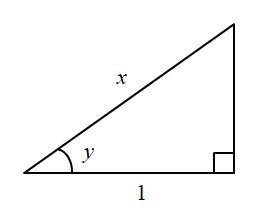
Using Pythagoras' Theorem the opposite side is $\sqrt{\mathstrut{x^2 - 1}}$.

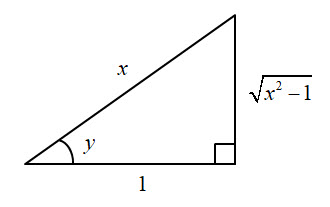
$$ \implies \text{sec }y \ = \ x \\[18pt] \implies \text{tan } \ y \ =\ \frac{\sqrt{\mathstrut{x^2 - 1}}}{1} \ \ = \ \ \sqrt{\mathstrut{x^2 - 1}}\\[18pt] \implies \frac{dy}{dx} = \frac{1}{x\ \sqrt{\mathstrut{x^2 - 1}} } \\[24pt] $$ Looking at the graph of the inverse function, we can see that the gradient is positive over the whole of the domain. So we have to modify our result by changing the $x$ to $|x|$ to ensure that it remains so. $$ \color{red}{\text{Hence if: }\quad y = \text{sec}^{-1}\ x \quad \text{then} \quad \frac{dy}{dx} \ = \ \frac{1}{|x| \ \sqrt{\mathstrut{x^2 - 1}}}} $$

IMPORTANT

As in the previous derivation, we still need to consider where $\large \frac{\pi}{2}\normalsize \ \lt \ y \ \le \ \pi$. There exists a triangle as shown below with sides such that $\text{sec }y = -x$. This time the angle is in the 2nd quadrant and the triangle can be drawn as:

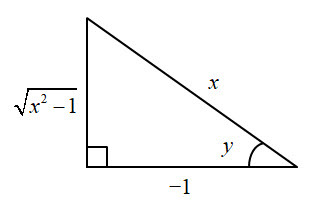
The opposite side this time is: $$ \sqrt{\mathstrut{x^2-1}}$$ and so: $$ \implies \frac{dy}{dx} = \frac{1}{x\ \sqrt{\mathstrut{x^2 - 1}} } \\[24pt] $$exactly the same as before. However, as $x$ is negative then this would change the sign of the derivative to a negative value.

So this is why we need to write $|x|$ in the formula to ensure that the derivative is always positive, irrespective of the sign of $x$.

$$ \color{red}{\text{Hence if: }\quad y = \text{sec}^{-1}\ x \quad \text{then} \quad \frac{dy}{dx} \ = \ \frac{1}{|x| \ \sqrt{\mathstrut{x^2 - 1}}}} $$

---

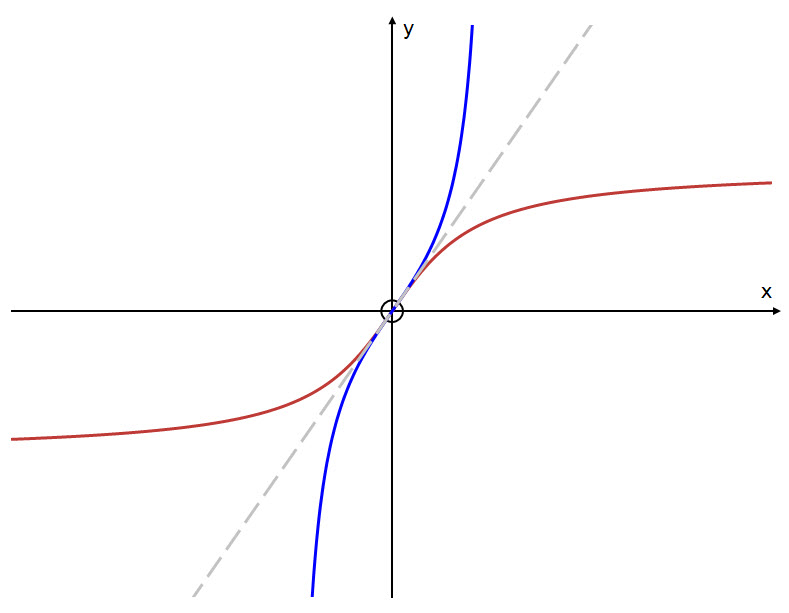
Graph of the Inverse Cotangent function

First we will look at the graph of $y = \text{cot }x$.

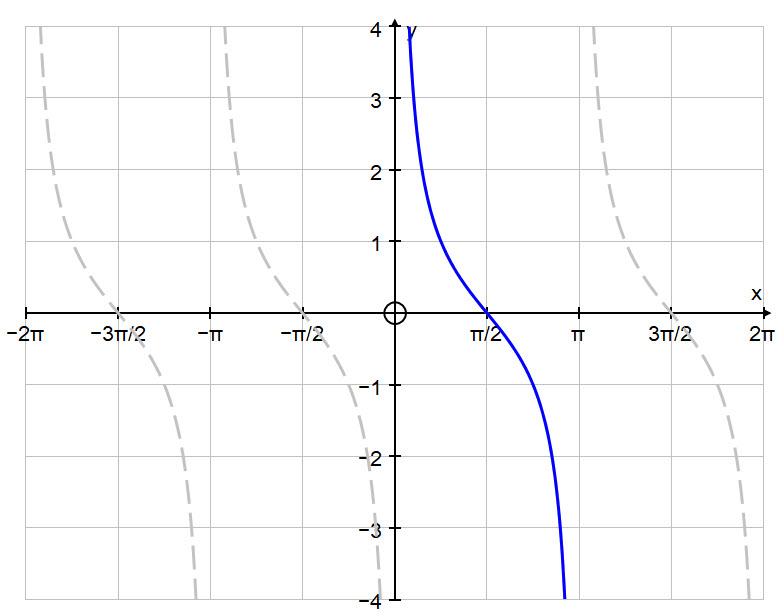
In order to make this function invertible, i.e. creating a one-to-one correspondence for an inverse function to exist, we have to restrict the domain to: $$0 \ \lt \ x \ \lt \ \pi $$

Reflect $y = \text{cot }x$ (in blue), in the line $y=x$ to obtain the graph of the inverse function $y\ = \text{cot}^{-1}\ x$ (in red):

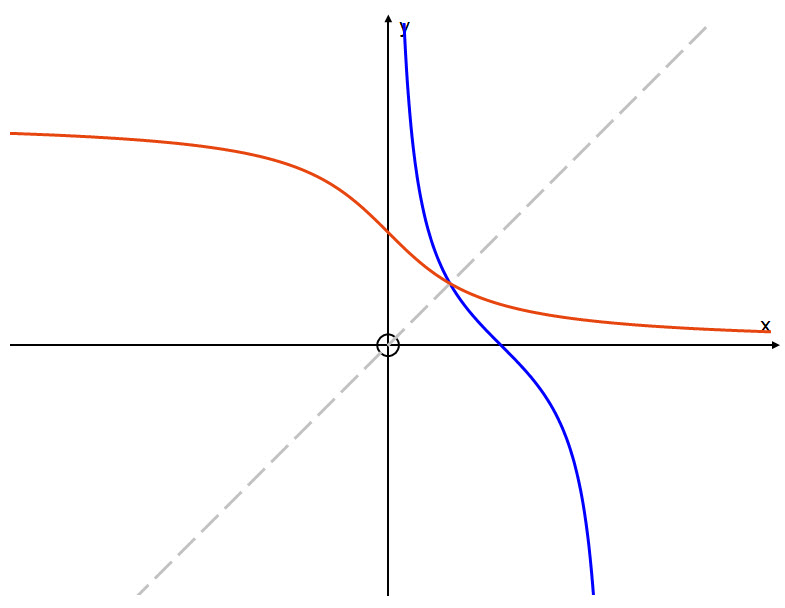
The domain of the inverse function is: $ x \in (-\infty,\ \infty)\ $

The range of the inverse function is: $ 0 \lt y \lt \pi $

Below is the graph of the inverse function: $\ y=\text{cot}^{-1}\ x $.

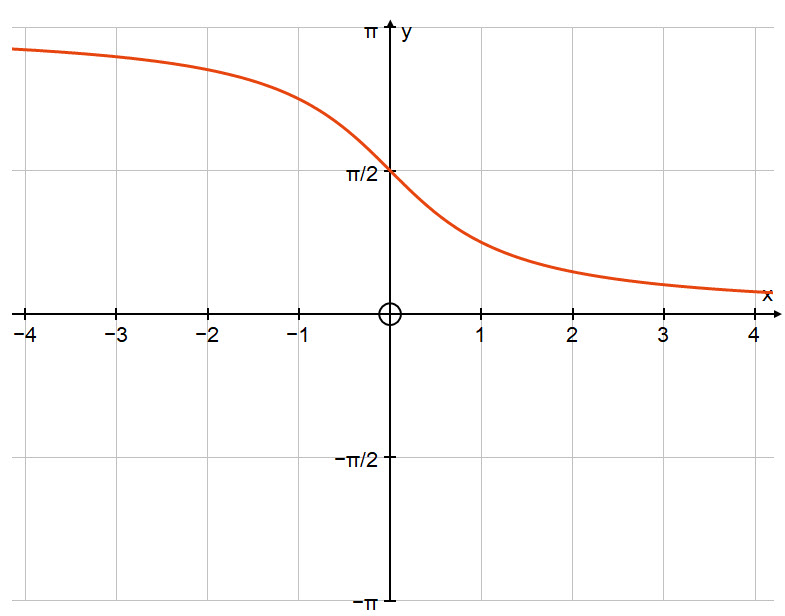
There are two schools of thought over the correct domain to use for $y=\text{cot }x$ in order for it to be invertible, and major mathematical software have differing views. We have chosen to use the domain shown above. If you want to find out more about these differing opinions, then click on the following link:  SquareCirclez

The Derivative of cot⁻¹ x

$$ \text{Let } \ \ y = \text{cot}^{-1}\ x \\[12pt] \implies \quad x = \text{cot }y \\[12pt] \implies \quad \frac{dx}{dy} \ = \ -\text{cosec}^2\ y \\[12pt] \implies \quad \frac{dy}{dx} \ = \ -\frac{1}{\text{cosec}^2\ y}\\[12pt] \implies \quad \frac{dy}{dx} \ = \ -\text{sin}^2\ y\\[12pt] $$Now we know that for $0\ \le \ y \ \lt \large \frac{\pi}{2}$ there exists a triangle as shown below with sides such that $\text{cot }y = x$:

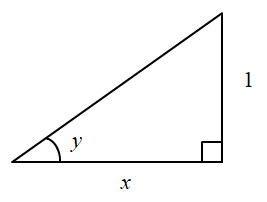
Using Pythagoras' Theorem the hypotenuse is $\sqrt{\mathstrut{1+x^2 }}$.

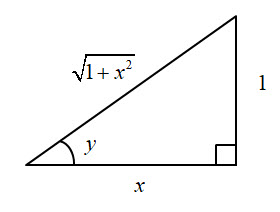
$$ \implies \text{cot }y \ = \ x \\[18pt] \implies \text{sin } \ y \ =\ \frac{1}{\sqrt{\mathstrut{1+x^2}}} \\[18pt] \implies \text{sin}^2 \ y \ = \ \frac{1}{1+x^2}\\[18pt] \implies \frac{dy}{dx} = -\frac{1}{1+x^2 } \\[24pt] \color{red}{\text{Hence if: }\quad y = \text{cot}^{-1}\ x \quad \text{then} \quad \frac{dy}{dx} \ = \ -\frac{1}{1+x^2}} $$

IMPORTANT

As in the previous derivation, we still need to consider where $\large \frac{\pi}{2}\normalsize \ \le \ y \ \lt \ \pi$. There exists a triangle as shown below with sides such that $\text{cot }y = -x$. This time the angle is in the 2nd quadrant and the triangle can be drawn as:

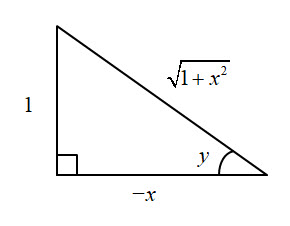
The hypotenuse is: $$ \sqrt{\mathstrut{1+x^2}}$$ and so: $$ \implies \frac{dy}{dx} = \frac{1}{1+x^2} \\[24pt] $$exactly the same as before. Note that the derivative is always negative. We can verify this as the gradient across the whole domain is always negative.

$$ \color{red}{\text{Hence if: }\quad y = \text{cot}^{-1}\ x \quad \text{then} \quad \frac{dy}{dx} \ = \ -\frac{1}{1+x^2 }} $$

---

Let's put these results together in a table and look at the pattern of the results.

We will add these results to our table of Standard Derivatives

Click the link to see: Standard Derivatives Table .

As this is a long lesson with lots of content, we shall leave the examples until the next lesson.

---

You should know how to restrict the domain of a trigonometric function in order for an inverse to exist.

You should be able to deduce the range of the function with the restricted domain.

You should be able to deduce the domain and range of the inverse function from the domain and range of the original function.

You should be familiar with the graphs of the inverse functions as a reflection of the original function in the line $y=x$.

You should be familiar with the derivatives of the inverse functions and how to derive them using the generic inverse function derivative.

Go to the next topic in the side menu to learn how to use the standard derivatives of Inverse Trigonometric Functions